Probability and Expected Value of Hearthstone Card Pack

Card Pack and Rarity

Hearthstone is a collectible card game developed by Blizzard Entertainment. Each Hearthstone game is played with a 30-card deck, made up entirely of cards that have been unlocked in the player's collection. These cards are divided into 5 rarity categories. Basic cards are cards that you are guaranteed to receive at the biginning. The other four rarities of cards correspond to the likelihood that the card will be opened up in a pack. Each card pack contains 5 cards. Common cards are the most likely to appear in a pack, followed by Rare cards, then Epic cards, then Legendary cards. On average, high rarity cards tend to be more powerful than low rarity cards. That's the reason why drawing a lengendary card from a pack is the dream for every Hearthstone player.

Arcane Dust Value

Arcane Dust is the resource players use to construct cards of their choice. Any card in your collection can be disenchanted and turned into Arcane Dust, rewarding an amount of Arcane Dust to the player depending on the card's rarity. The value of differnet type of cards can be viewed below.

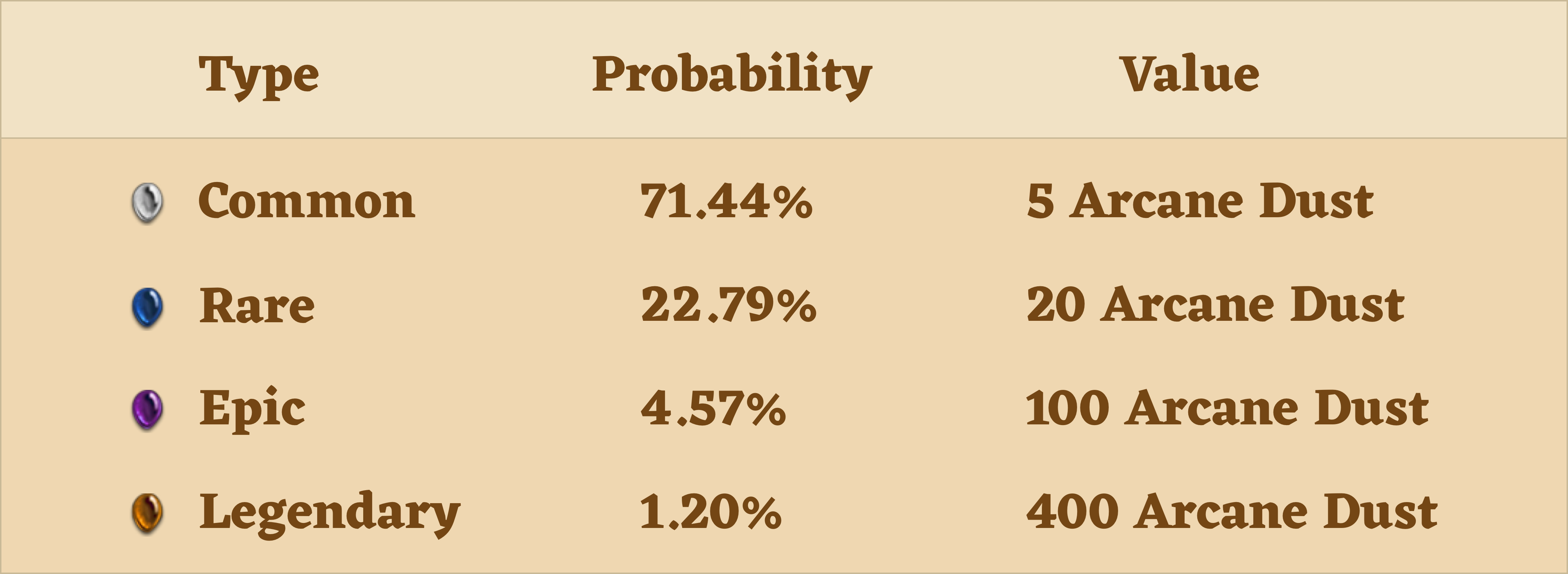
Probability

Though everyone wants to draw a legendary card when openning the pack. Making predictions about something, like when will I get my next legendary card, is always a difficult task. However, with the probability theory, we can provide the best estimate of the chacne that you will get a lengendary card in your next 5-card pack. The probability of an event is a number indicating how likely that event will occur. This number is always between 0 and 1, where 0 indicates impossibility and 1 indicates certainty.

For example, we have known the probability of drawing a legendary card is 1.20%. In an actual series of pack opens, we may get more or less than exactly 1.20% legendary cards or 71.44% commmon cards. But as the number of opens increases, the long-run frequency of the legendary card is bound to get closer and closer to 1.20%, which means if you repeatedly open packs many times, you would expect about about 1.2% of the cards to be legendary.

Expected Value

Consider the outcome of a single pack open, and call it X. A reasonable question you might ask is “What is the average value of X?". We define this notion of “average” as a weighted sum of outcomes. Since the X can on four values, each has its own probability, the weighted average of these outcomes should be

This may seem dubious. How can the average roll be a noninteger value? The confusion lies in the interpretation of the phrase average dust value. A more correct interpretation would be the long term average of the card draws. Suppose we opened the packs many times, and recorded each card. Then we took the average of all those cards and will find this is exactly the computation we have done above! In the long run, the fraction of each of these outcomes is nothing but their probability, in this case, 1.20% for each of the lengendary card outcomes. From this very specific die rolling example, we can abstract the notion of the average value of a random quantity. The concept of average value is an important one in statistics, so much so that it even gets a special bold faced name. Below is the mathematical definition for the expectation, or average value, of a random quantity X.

The expected value, or expectation of X, denoted by E(X), is defined to be

Consider the probabilistic experiment of opening a card pack and watch as the running sample mean converges to the expected dust value of 17.5.

The right table shows the likelihood of any single card being of a given rarity. And feel free to adjust the bar to change the distribution and observe how this hanges the expectation!